PyJive workshop: stability of a house-shaped frame

PyJive workshop: stability of a house-shaped frame#

Case definition#

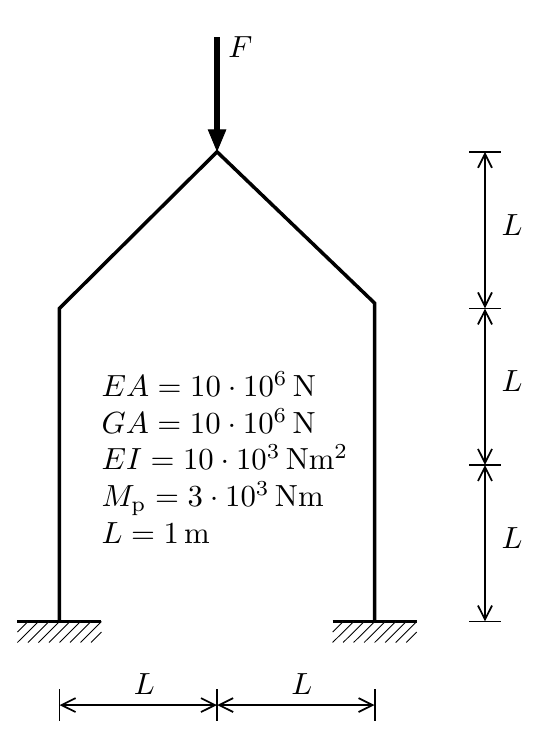
In this workshop, you are asked to set up your own problem and analyse it from different angles, using the FrameModel and different modules from pyJive as discussed in previous workshops. The case that is studied is the one illustrated below.

Simple frame
import matplotlib.pyplot as plt
import numpy as np

import os
import sys

pyjivepath = '../../../pyjive/'
sys.path.append(pyjivepath)

if not os.path.isfile(pyjivepath + 'utils/proputils.py'):
    print('\n\n**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**\n\n')
    raise Exception('pyjive not found')

from utils import proputils as pu
import main
from names import GlobNames as gn

%matplotlib widget

**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**

---------------------------------------------------------------------------
Exception                                 Traceback (most recent call last)
Cell In[1], line 12
     10 if not os.path.isfile(pyjivepath + 'utils/proputils.py'):
     11     print('\n\n**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**\n\n')
---> 12     raise Exception('pyjive not found')
     14 from utils import proputils as pu
     15 import main

Exception: pyjive not found

Linear elastic analysis#

Define your own pair of geometry file and input file and perform a linear elastic analysis. A good starting point could be the frameNonlin.pro input file from the workhop on buckling. Make sure you switch off nonlinearity.

props = pu.parse_file('house-linear.pro')
globdat = main.jive(props)

Storing results#

Below, a function is defined to looks up load-displacement data from globdat. The function is then called to store the data from the linear elastic analysis. This can later be used to compare the results from different analyses in a single diagram.

You need to modify the function to get relevant load/displacement data. Note that in order to record data for a particular node group, you need to specify this group in the loaddisp part of the .pro-file.

def getFu(globdat):
    F = abs(globdat['loaddisp']['top']['load']['dy'])
    u = abs(globdat['loaddisp']['top']['disp']['dy'])
    return np.vstack((u,F))

lin_elas = getFu(globdat)

# pad with zeros because linear elastic gives only one force-displacement point
lin_elas = np.hstack((np.zeros((2,1)), lin_elas))

Linear buckling analysis#

Now perform linear buckling analysis. You are recommended to make a new input file because quite several modifications need to be made. Again, you can take one from the buckling workshop as starting point.

props = pu.parse_file('house-lb.pro')
globdat = main.jive(props)
bucklingLoad = globdat[gn.LBFACTORS][0]

Geometrically nonlinear elastic analysis#

The next step is to perform geometrically nonlinear elastic anlaysis. You can take the input file from the linear-elastic analysis and overwrite one of the entries in the notebook. How do the results compare to the results from linear buckling analysis (in terms of buckling load and buckling mode)?

props = pu.parse_file('house-nonlin.pro')
globdat = main.jive(props)

Geometrically linear elastic/plastic analysis#

Next, perform a geometrically linear analysis with plastic hinges. Again, take the previous input file as starting point.

Geometrically nonlinear elastic/plastic analysis#

As last analysis, perform a complete nonlinear finite element simulation with geometric nonlinearity and plastic hinges.

Comparison with results#

Finally, compare the results from different analysis. Also include the rigid-plastic 2nd order analysis result (see pdf for background):

\[ F \approx \frac{6M_\mathrm{p}}{L}\left(1-2\textstyle\frac13\theta\right) \]

Suppose you want to check this analytical solution, what can you change to the model inputs to get more definite insight in its validity?

Contents